[ English | Japanese ]
Software
This page is outdated. For more recent software on reliable and robust machine learning, please see here, which is maintained by Imperfect Information Learning Team, Center for Advanced Intelligence Project (AIP), RIKEN.The software available below is free of charge for research and education purposes. However, you must obtain a license from the author(s) to use it for commercial purposes. The software must not be distributed without prior permission of the author(s).
The software is supplied "as is" without warranty of any kind, and the author(s) disclaim any and all warranties, including but not limited to any implied warranties of merchantability and fitness for a particular purpose, and any warranties or non infringement. The user assumes all liability and responsibility for use of the software and in no event shall the author(s) be liable for damages of any kind resulting from its use.
Fundamentals
- Density ratio estimation
- KLIEP (Kullback-Leibler importance estimation procedure): MATLAB
- GM-KLIEP (Gaussian-mixture KLIEP): MATLAB (by Makoto Yamada)
- LSIF (least-squares importance fitting): R (by Takafumi Kanamori)
- uLSIF (unconstrained LSIF): MATLAB, R (by Takafumi Kanamori), C++ (by Issei Sato)
- RuLSIF (relative uLSIF): MATLAB (by Makoto Yamada), R (by Max Wornowizki), Python (by Song Liu)
- Density difference estimation
- LSDD (least-squares density difference): MATLAB, Python (by Marthinus Christoffel du Plessis)
- Density derivative estimation
- LSLDG (least-squares log-density gradient): MATLAB (by Hiroaki Sasaki)
- Mutual information estimation
- MLMI (maximum-likelihood mutual information): MATLAB (with Taiji Suzuki)
- LSMI (least-squares mutual information): MATLAB (with Taiji Suzuki)
- LSMI (multiplicative kernel model): MATLAB (by Tomoya Sakai)
- LSQMI (least-squares quadratic mutual information): MATLAB
- Hetero-distributional subspace search
- LHSS (least-squares hetero-distributional search): MATLAB (with Makoto Yamada)
Applications
- Covariate shift adaptation
- IWLS+IWCV+uLSIF (importance-weighted least-squares + importance-weighted cross-validation + unconstrained least-squares importance fitting): MATLAB
- IWLR+KLIEP (importance-weighted logistic regression + Kullback-Leibler importance estimation procedure): MATLAB (by Makoto Yamada)
- IWLSPC+IWCV+KLIEP (importance-weighted least-squares probabilistic classifier + importance-weighted cross-validation + Kullback-Leibler importance estimation procedure): MATLAB (by Hirotaka Hachiya)
- Class prior change adaptation
- uLSIF-based method: MATLAB (by Marthinus Christoffel du Plessis)
- LSDD-based method: MATLAB (by Marthinus Christoffel du Plessis)
- Inlier-based outlier detection
- MLOD (maximum-likelihood outlier detection): MATLAB
- LSOD (least-squares outlier detection): MATLAB
- LSAD (least-squares anomaly detection): Python (by John Quinn)
- Feature selection
- MLFS (maximum-likelihood feature selection in supervised regression/classification): MATLAB (with Taiji Suzuki)
- LSFS (least-squares feature selection in supervised regression/classification): MATLAB (with Taiji Suzuki)
- L1-LSMI (L1-LSMI-based feature selection for supervised regression/classification): MATLAB (by Wittawat Jitkrittum)
- HSIC-LASSO (Hilbert-Schmidt independence criterion + least absolute shrinkage and selection operator for high-dimensional feature selection in supervised regression/classification): MATLAB (by Makoto Yamada)
- Dimensionality reduction/feature extraction/metric learning
- NGCA (non-Gaussian component analysis, unsupervised linear dimensionality reduction): MATLAB (by Gilles Blanchard)
- LSDR (least-squares dimensionality reduction, supervised linear dimensionality reduction for regression/classification): MATLAB (with Taiji Suzuki)
- SCA (sufficient component analysis, supervised linear dimensionality reduction for regression/classification): MATLAB (by Makoto Yamada)
- LSQMID (least-squares quadratic mutual information derivative, supervised linear dimensionality reduction for regression/classification): MATLAB (by Voot Tangkaratt)
- LFDA (local Fisher discriminant analysis, supervised linear dimensionality reduction for classification): MATLAB
- SELF (semi-supervised LFDA, semi-supervised linear dimensionality reduction for classification): MATLAB
- LSCDA (least-squares canonical dependency analysis, linear dimensionality reduction for paired data): MATLAB (by Masayuki Karasuyama)
- SERAPH (semi-supervised metric learning paradigm with hyper-sparsity, semi-supervised metric learning for classification): MATLAB (by Gang Niu)
- Classification
- Conditinonal probability estimation
- LSCDE (least-squares conditional density estimation): MATLAB
- LSPC (least-squares probabilitic classifier): MATLAB, Python (by John Quinn)
- SMIR (squared-loss mutual information regularization, semi-supervised probabilistic classification): MATLAB (by Gang Niu and by Wittawat Jitkrittum)
- Independence test
- LSIT (least-squares independence test): MATLAB
- Two-sample test
- LSTT (least-squares two-sample test): MATLAB
- Change detection
- CD-RuLSIF (distributional change detection by RuLSIF): MATLAB (by Song Liu)
- CD-KLIEP (structural change detection by sparse KLIEP): MATLAB (by Song Liu)
- Clustering
- Independent component analysis
- LICA (independent component analysis): MATLAB (by Taiji Suzuki)
- Causal direction inference
- LSIR (least-squares independence regression): MATLAB (by Makoto Yamada)
- Cross-domain object matching
- LSOM (least-squares object matching): MATLAB (by Makoto Yamada)
- Hidden Markov Model
- DRHMM (density-ratio hidden Markov model): MATLAB and Python (by John Quinn)
- Sparse learning
- DAL (l1/grouped-l1/trace-norm regularization solver): MATLAB (by Ryota Tomioka)
- Matrix/tensor factorization
- VBMF (variational Bayesian matrix factorization): MATLAB
- Multitask learning with tensor factorization: MATLAB (by Kishan Wimalawarne)
- Reinforcement learning
- IW-PGPE-OB (model-free policy gradient method with sample reuse): MATLAB
- Crowdsourcing
- BBTA (bandit-based task assignment): Python (by Hao Zhang)
Kullback-Leibler Importance Estimation Procedure (KLIEP)
- Kullback-Leibler Importance Estimation Procedure (KLIEP) is an algorithm to directly estimate the ratio of two density functions without going through density estimation. The optimization problem involved with KLIEP is convex so the unique global optimal solution can be obtained. Furthermore, the KLIEP solution tends to be sparse, which contributes to reducing the computation time.
-
MATLAB implementation of KLIEP:
KLIEP.zip
- "KLIEP.m" is the main function.
- "demo_KLIEP.m" is a demo script.
-
Examples:
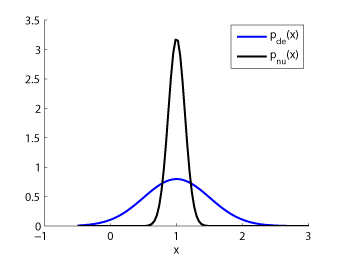
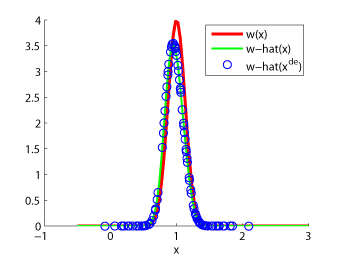
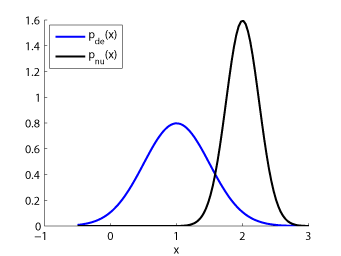
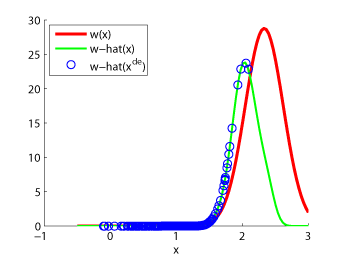
-
References:
-
Sugiyama, M., Suzuki, T., Nakajima, S., Kashima, H., von Bünau, P. & Kawanabe, M.
Direct importance estimation for covariate shift adaptation.
Annals of the Institute of Statistical Mathematics, vol.60, no.4, pp.699-746, 2008.
[ paper ] -
Sugiyama, M., Nakajima, S., Kashima, H., von Bünau, P. & Kawanabe, M.
Direct importance estimation with model selection and its application to covariate shift adaptation.
In J. C. Platt, D. Koller, Y. Singer, and S. Roweis (Eds.), Advances in Neural Information Processing Systems 20, pp.1433-1440, Cambridge, MA, MIT Press, 2008.
(Presented at Neural Information Processing Systems (NIPS2007), Vancouver, B.C., Canada, Dec. 3-8, 2007.)
[ paper, poster ]
-
Sugiyama, M., Suzuki, T., Nakajima, S., Kashima, H., von Bünau, P. & Kawanabe, M.
Unconstrained Least-Squares Importance Fitting (uLSIF)
- Unconstrained Least-Squares Importance Fitting (uLSIF) is an algorithm to directly estimate the ratio of two density functions without going through density estimation. The solution of uLSIF as well as the leave-one-out score can be computed analytically, thus uLSIF is computationally very efficient and stable. Furthermore, the uLSIF solution tends to be sparse, which contributes to reducing the computation time.
-
MATLAB implementation of uLSIF:
uLSIF.zip
- "uLSIFP.m" is the main function.
- "demo_uLSIF.m" is a demo script.
-
Examples:
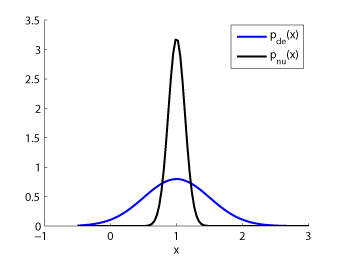
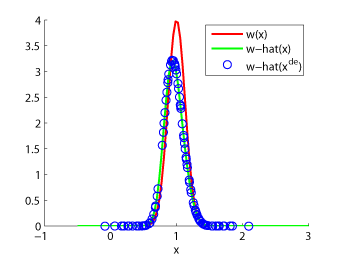
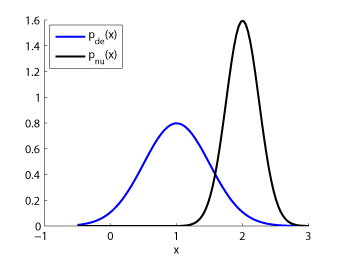
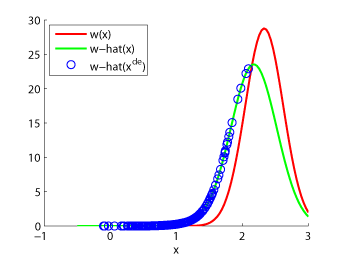
-
References:
-
Kanamori, T., Hido, S., & Sugiyama, M.
A least-squares approach to direct importance estimation.
Journal of Machine Learning Research, vol.10 (Jul.), pp.1391-1445, 2009.
[ paper ] -
Kanamori, T., Hido, S., & Sugiyama, M.
Efficient direct density ratio estimation for non-stationarity adaptation and outlier detection,
In D. Koller, D. Schuurmans, Y. Bengio, L. Botton (Eds.), Advances in Neural Information Processing Systems 21, pp.809-816, Cambridge, MA, MIT Press, 2009.
(Presented at Neural Information Processing Systems (NIPS2008), Vancouver, B.C., Canada, Dec. 8-13, 2008.)
[ paper, poster ]
-
Kanamori, T., Hido, S., & Sugiyama, M.
Least-Squares Density-Difference (LSDD)
- Least-Squares Density-Difference (LSDD) is an estimator of the difference between two densities, which could be used for, e.g., approximating the L2-distance.
-
MATLAB implementation of LSDD:
LSDD.zip
- "LSDD.m" is the main function.
- "demo_LSDD.m" is a demo script.
- "lsdd.py" is the main function.
- "demo_lsdd.py" is a demo script.
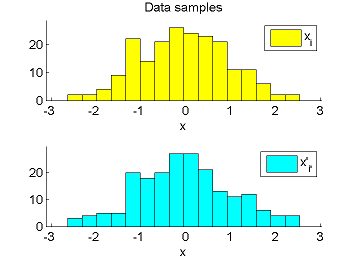
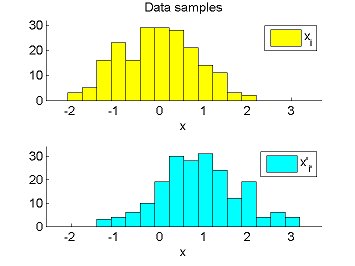
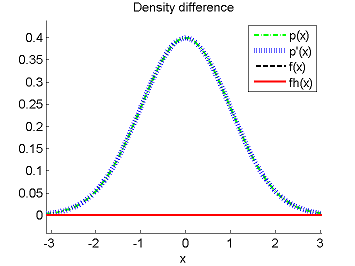
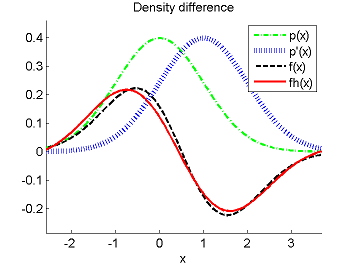
-
Sugiyama, M., Suzuki, T., Kanamori, T., Du Plessis, M. C., Liu, S., & Takeuchi, I.
Density-difference estimation.
Neural Computation, vol.25, no.10, pp.2734-2775, 2013.
[ paper ] -
Sugiyama, M., Suzuki, T., Kanamori, T., du Plessis, M. C., Liu, S., & Takeuchi, I.
Density-difference estimation.
In P. Bartlett, F. C. N. Pereira, C. J. C. Burges, L. Bottou, and K. Q. Weinberger (Eds.), Advances in Neural Information Processing Systems 25, pp.692-700, 2012.
(Presented at Neural Information Processing Systems (NIPS2012), Lake Tahoe, Nevada, USA, Dec. 3-6, 2012)
[ paper, poster ]
Least-Squares Log-Density Gradient (LSLDG)
- Least-Squares Log-Density Gradient (LSLDG) is an algorithm which directly estimates the gradient of a log-density without going through density estimation. The solution is computed analytically.
-
The application of LSLDG is clustering based on mode
seeking. The clustering method has the following advantages:
- We do not need to set the number of clusters in advance.
- All the parameters (e.g. bandwidth) can be optimized by cross validation.
- It works significantly better than mean-shift clustering in high-dimensional data.
-
MATLAB implementation of LSLDG:
LSLDG.zip
- "demo_LSLDG.m" is a demo script for log-density gradient estimation.
- "demo_LSLDGClust.m" is a demo script for clustering.
-
Examples:
- Log-density gradient estimation.
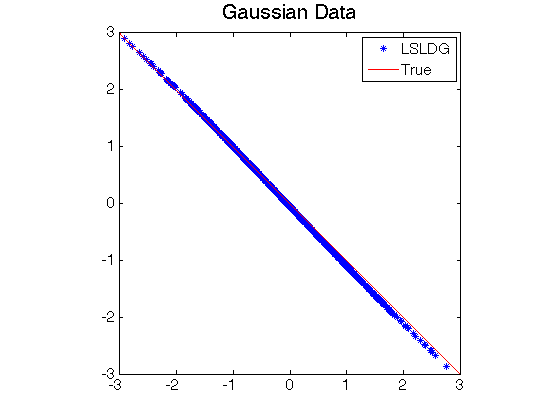
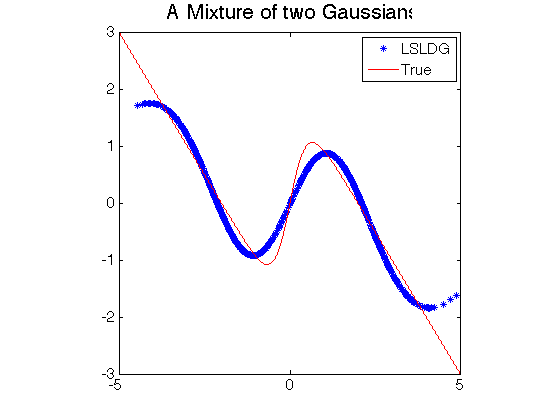
- Clustering by seeking modes.
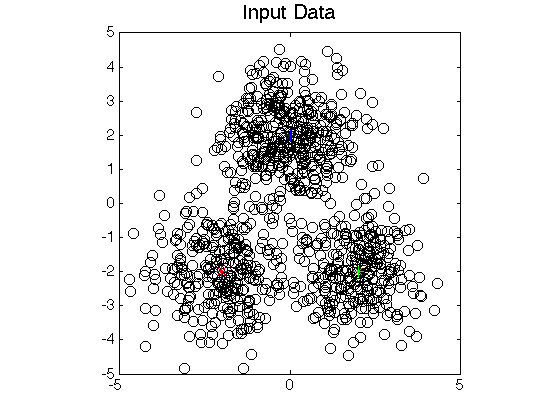
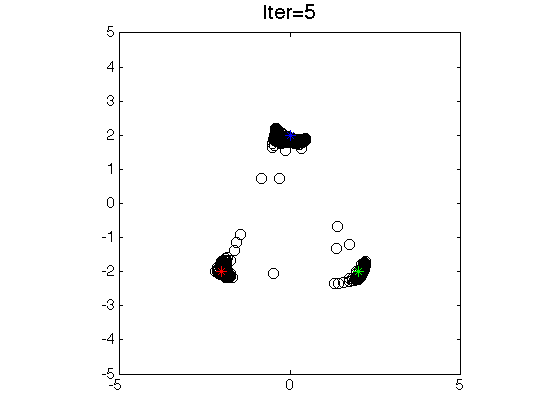
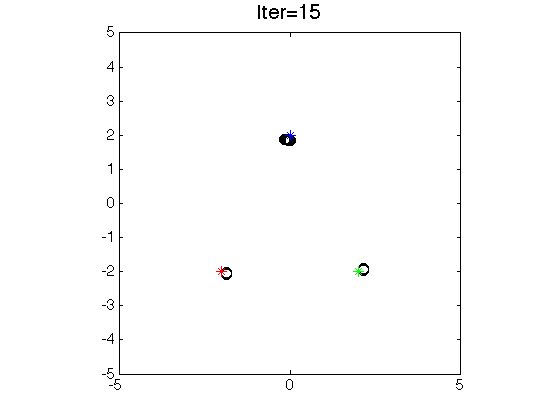
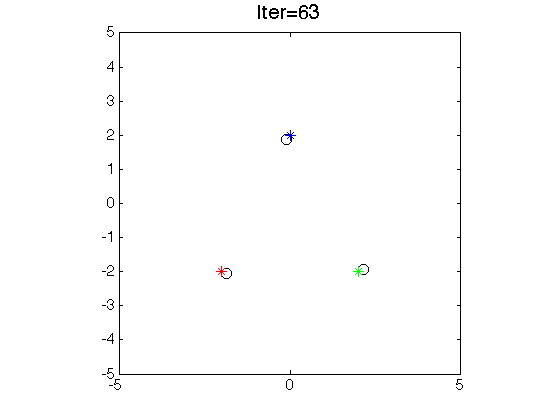
-
References:
-
Sasaki, H., Hyvärinen, A., & Sugiyama, M.
Clustering via mode seeking by direct estimation of the gradient of a log-density.
In T. Calders, F. Esposito, E. Hullermeier, and R. Meo (Eds.), Machine Learning and Knowledge Discovery in Databases, Part III, Lecture Notes in Computer Science, vol.8725, pp.19--34, Berlin, Springer, 2014.
(Presented at the European Conference on Machine Learning and Principles and Practice of Knowledge Discovery in Databases (ECML-PKDD2014), Nancy, France, Sep. 15-19, 2014)
[ paper ]
-
Sasaki, H., Hyvärinen, A., & Sugiyama, M.
Maximum Likelihood Mutual Information (MLMI)
- Maximum Likelihood Mutual Information (MLMI) is an estimator of mutual information based on the density-ratio estimation method KLIEP. A mutual information estimator could be used as a measure of statistical independence between random variables (smaller is more independent).
-
MATLAB implementation of MLMI:
MLMI.zip
- "MLMI.m" is the main function.
- "demo_MLMI.m" is a demo script.
-
Examples:
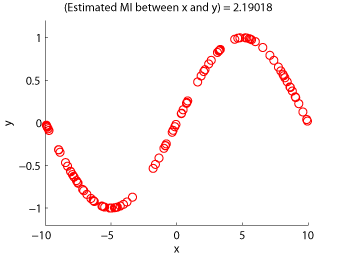
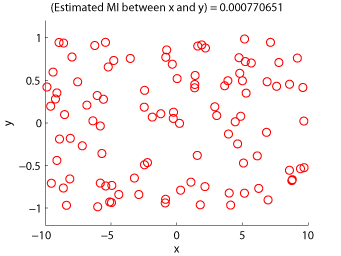
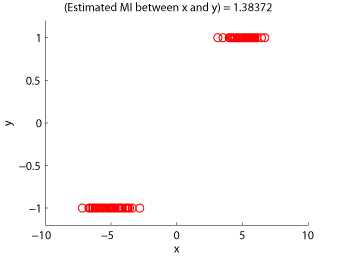
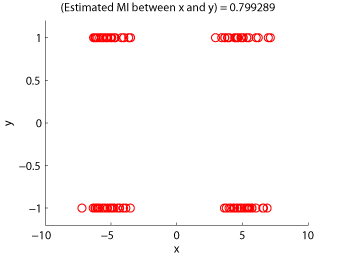
-
References:
-
Suzuki, T., Sugiyama, M., & Tanaka, T.
Mutual information approximation via maximum likelihood estimation of density ratio.
In Proceedings of 2009 IEEE International Symposium on Information Theory (ISIT2009), pp.463-467, Seoul, Korea, Jun. 28-Jul. 3, 2009.
[ paper ] -
Suzuki, T., Sugiyama, M., Sese, J. & Kanamori, T.
Approximating mutual information by maximum likelihood density ratio estimation.
In Y. Saeys, H. Liu, I. Inza, L. Wehenkel and Y. Van de Peer (Eds.), Proceedings of the Workshop on New Challenges for Feature Selection in Data Mining and Knowledge Discovery 2008 (FSDM2008) , JMLR Workshop and Conference Proceedings, vol. 4, pp.5-20, 2008.
[ paper ]
-
Suzuki, T., Sugiyama, M., & Tanaka, T.
Least-Squares Mutual Information (LSMI)
- Least-Squares Mutual Information (LSMI) is an estimator of a squared-loss variant of mutual information based on the density-ratio estimation method uLSIF. A mutual information estimator could be used as a measure of statistical independence between random variables (smaller is more independent).
-
MATLAB implementation of LSMI for plain kernel models:
LSMI.zip
- "LSMIregression.m" and "LSMIclassification.m" are the main functions.
- "demo_LSMI.m" is a demo script.
-
MATLAB implementation of LSMI for multiplicative kernel models:
mLSMI.zip
- "mLSMI.m" is the main function.
- "demo_mLSMI.m" is a demo script.
-
Examples:
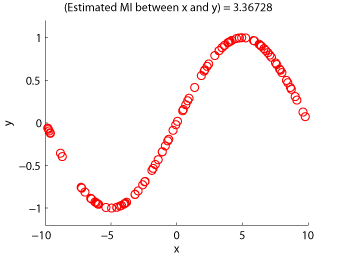
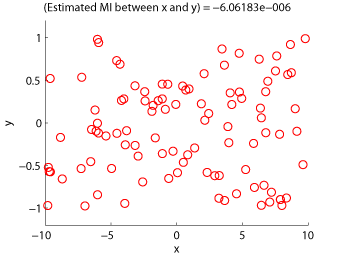
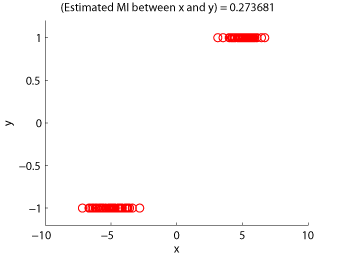
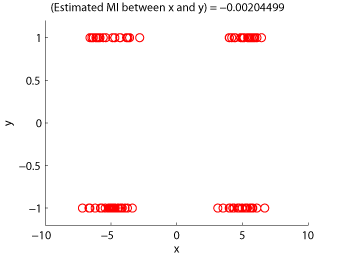
-
References:
-
Suzuki, T., Sugiyama, M., Kanamori, T., & Sese, J.
Mutual information estimation reveals global associations between stimuli and biological processes.
BMC Bioinformatics, vol.10, no.1, pp.S52, 2009.
[ paper ] -
Sakai, T. & Sugiyama, M.
Computationally efficient estimation of squared-loss mutual information with multiplicative kernel models.
IEICE Transactions on Information and Systems, vol.E97-D, no.4, pp.968-971, 2014.
[ paper ]
-
Suzuki, T., Sugiyama, M., Kanamori, T., & Sese, J.
Least-Squares Quadratic Mutual Information (LSQMI)
- Least-Squares Quadratic Mutual Information (LSQMI) is an estimator of a L2-loss variant of mutual information called quadratic mutual information (QMI) based on the density-difference estimation method LSDD. An QMI estimator could be used as a measure of statistical independence between random variables (smaller is more independent).
-
MATLAB implementation of LSQMI:
LSQMI.zip
- "LSQMIregression.m" and "LSQMIclassification.m" are the main functions.
- "demo_LSQMI.m" is a demo script.
-
Examples:
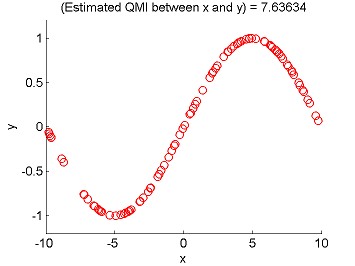
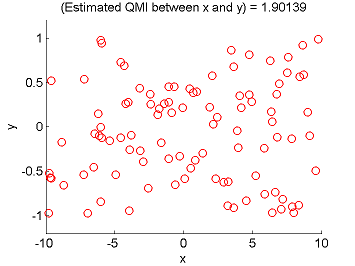
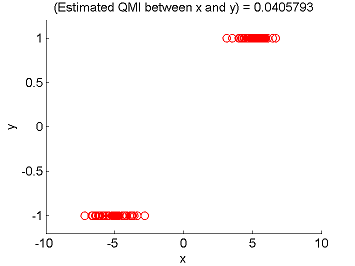
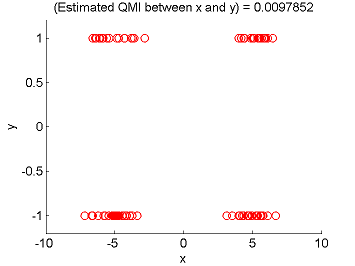
- References:
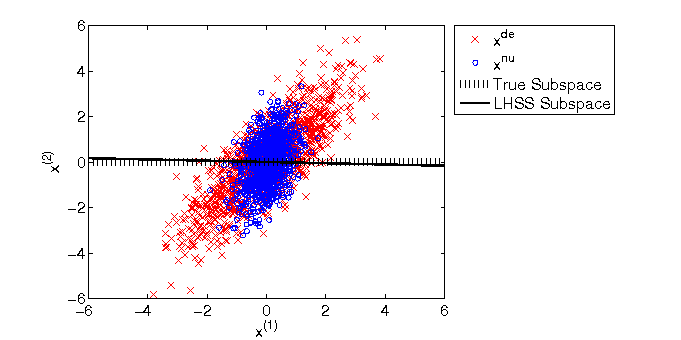
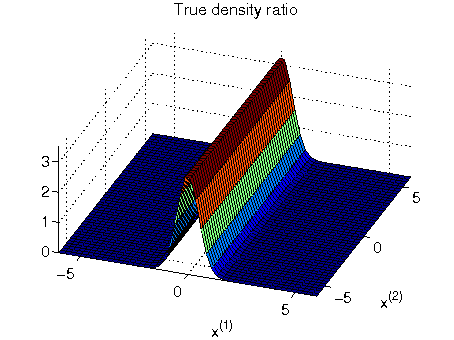
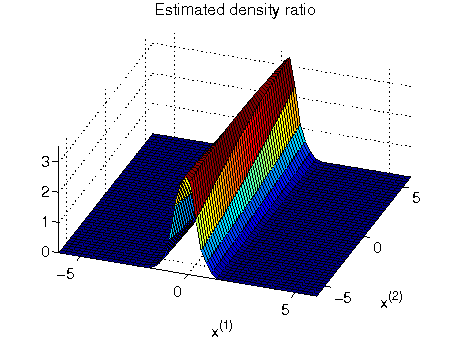
Least-squares Hetero-distributional Subspace Search (LHSS)
- Least-squares Hetero-distributional Subspace Search (LHSS) is an algorithm to find a subspace in which two probability distributions are similar (which is called the hetero-distributional subspace). LHSS can be used for improving the accuracy of direct density ratio estimatoin in high dimensions: first identify the hetero-distributional subspace by LHSS and then perform density ratio estimation only in the hetero-distributional subspace. This is called direct density-ratio estimation with dimensionality reduction (D3).
-
MATLAB implementation of LHSS:
LHSS.zip
- "demo_LHSS.m" is a demo script.
- "LHSS_train.m" is the function to find the hetero-distributional subspace.
- "LHSS_test.m" is the function to estimate the density ratio based on LHSS.
-
Examples:
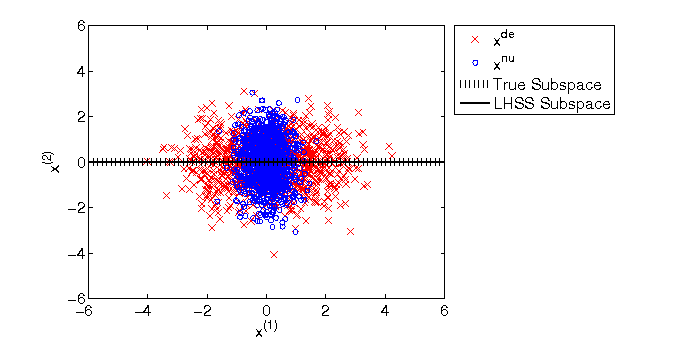
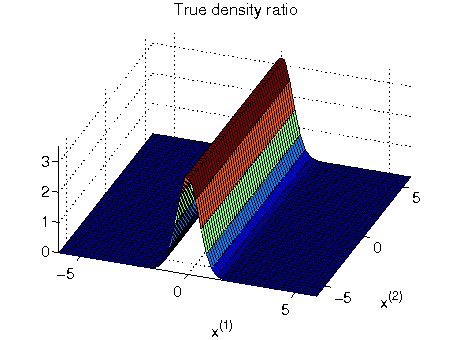
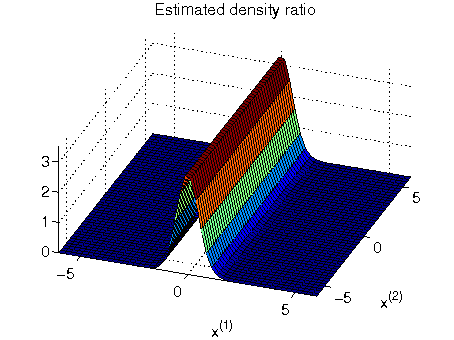
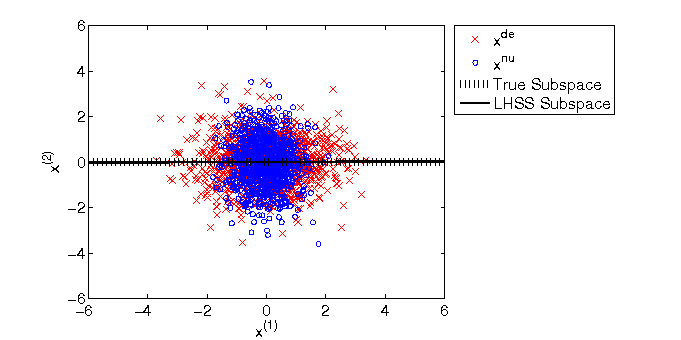
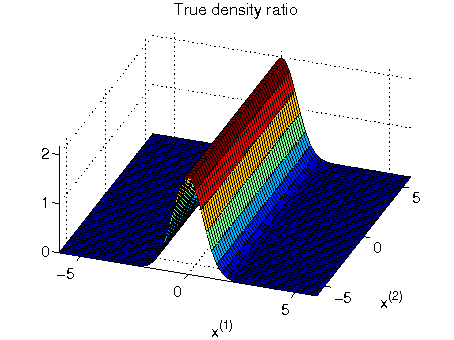
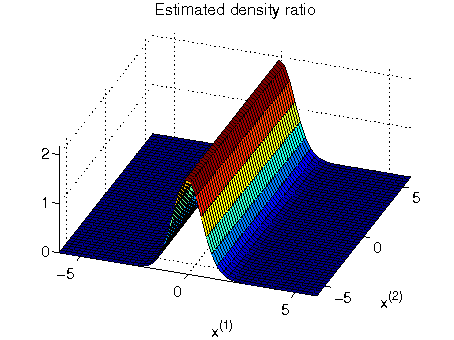
-
References:
-
Sugiyama, M., Yamada, M., von Bünau, P., Suzuki, T., Kanamori, T., & Kawanabe, M.
Direct density-ratio estimation with dimensionality reduction via least-squares hetero-distributional subspace search.
Neural Networks, vol.24, no.2, pp.183-198, 2011.
[ paper ]
-
Sugiyama, M., Yamada, M., von Bünau, P., Suzuki, T., Kanamori, T., & Kawanabe, M.
Importance-Weighted Least-Squares (IWLS)
-
Importance-Weighted Least-Squares (IWLS)
is an importance-weighted version of regularized kernel least-squares
for covariate shift adaptation,
where the training and test input distributions differ
but the conditional distribution of outputs given inputs
is unchanged between training and test phases.
uLSIF is used for importance estimation,
and
Importance-Weighted Cross-Validation (IWCV) is used for model selection.
-
MATLAB implementation of IWLS:
IWLS.zip
- "demo_IWLS.m" is a demo script.
-
Examples:
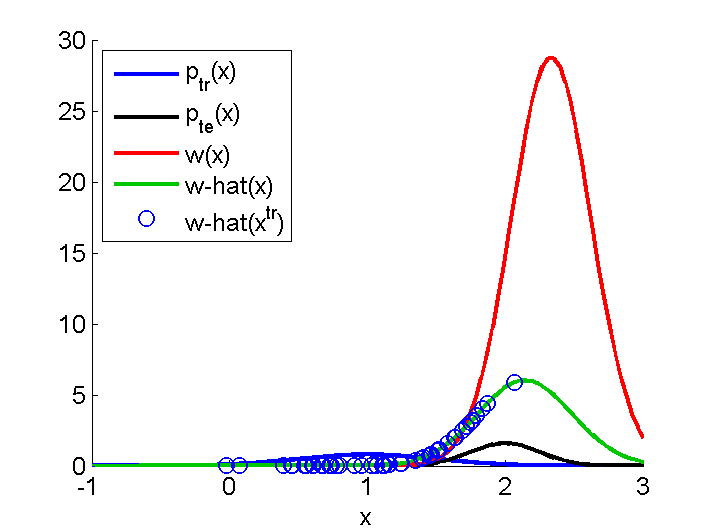
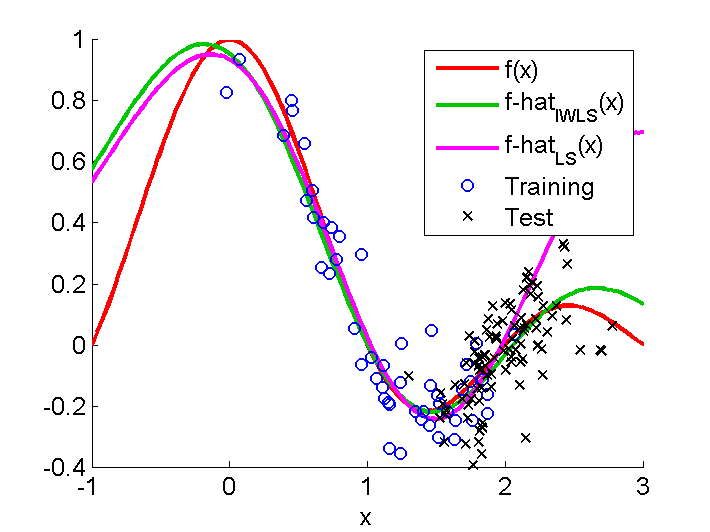
-
References:
-
Kanamori, T., Hido, S., & Sugiyama, M.
A least-squares approach to direct importance estimation.
Journal of Machine Learning Research, vol.10 (Jul.), pp.1391-1445, 2009.
[ paper ] -
Sugiyama, M., Krauledat, M., & Müller, K.-R.
Covariate shift adaptation by importance weighted cross validation.
Journal of Machine Learning Research, vol.8 (May), pp.985-1005, 2007.
[ paper ]
-
Kanamori, T., Hido, S., & Sugiyama, M.
Importance-Weighted Least-Squares Probabilistic Classifier (IWLSPC)
- The Importance-Weighted Least-Squares Probabilistic Classifier (IWLSPC) is an importance-weighted version of the LSPC for covariate shift adaptation, where training and test input distributions differ but the conditional distribution of outputs given inputs is unchanged between the training and test phases. uLSIF is used for importance estimation, and Importance-Weighted Cross-Validation (IWCV) is used for model selection.
-
MATLAB implementation of IWLSPC:
IWLSPC.zip
- "demo_IWLSPC.m" is a demo script.
-
Examples:
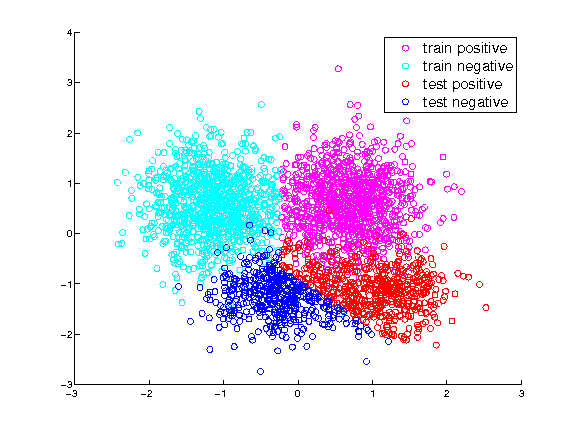
Training and test samples
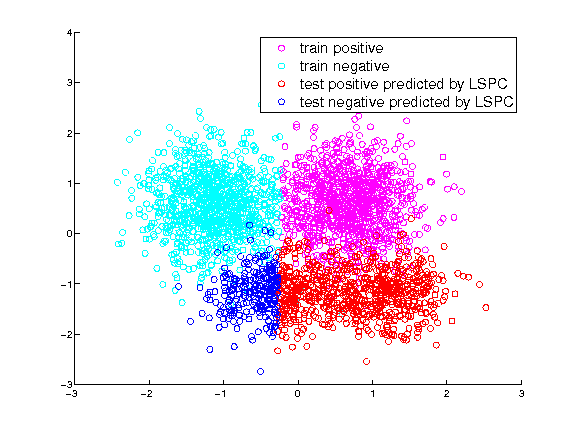
Training and test labels predicted by plain LSPC
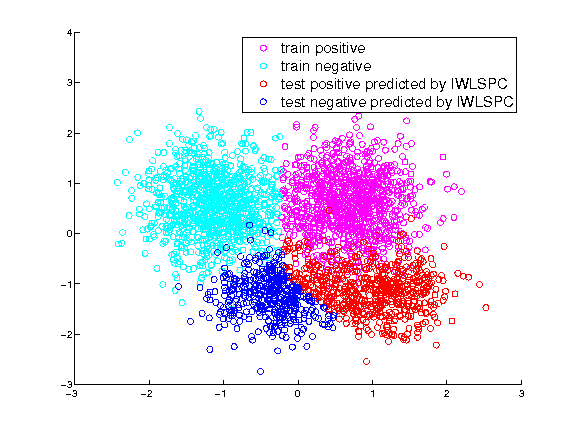
Training and test labels predicted by IWLSPC
-
References:
-
Hachiya, H., Sugiyama, M., & Ueda, N.
Importance-weighted least-squares probabilistic classifier for covariate shift adaptation with application to human activity recognition.
Neurocomputing, vol.80, pp.93-101, 2012.
[ paper ] -
Kanamori, T., Hido, S., & Sugiyama, M.
A least-squares approach to direct importance estimation.
Journal of Machine Learning Research, vol.10 (Jul.), pp.1391-1445, 2009.
[ paper ] -
Sugiyama, M., Krauledat, M., & Müller, K.-R.
Covariate shift adaptation by importance weighted cross validation.
Journal of Machine Learning Research, vol.8 (May), pp.985-1005, 2007.
[ paper ]
-
Hachiya, H., Sugiyama, M., & Ueda, N.
Maximum Likelihood Outlier Detection (MLOD)
- Maximum Likelihood Outlier Detection (MLOD) is an inlier-based outlier detection algorithm. The problem of inlier-based outlier detection is to find outliers in a set of samples (called the evaluation set) using another set of samples which consists only of inliers (called the model set). MLOD orders the samples in the evaluation set according to their degree of outlyingness. The degree of outlyingness is measured by the ratio of probability densities of evaluation and model samples. The ratio is estimated by the density-ratio estimation method KLIEP.
-
MATLAB implementation of MLOD:
MLOD.zip
- "MLOD.m" is the main function.
- "demo_MLOD.m" is a demo script.
-
Examples:
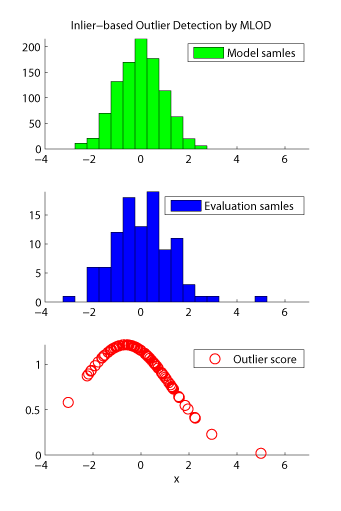
-
References:
-
Hido, S., Tsuboi, Y., Kashima, H., Sugiyama, M., & Kanamori, T.
Statistical outlier detection using direct density ratio estimation.
Knowledge and Information Systems, vol.26, no.2, pp.309-336, 2011.
[ paper ] -
Sugiyama, M., Suzuki, T., Nakajima, S., Kashima, H.,
von Bünau, P. & Kawanabe, M.
Direct importance estimation for covariate shift adaptation.
Annals of the Institute of Statistical Mathematics, vol.60, no.4, pp.699-746, 2008.
[ paper ]
-
Hido, S., Tsuboi, Y., Kashima, H., Sugiyama, M., & Kanamori, T.
Least-Squares Outlier Detection (LSOD)
- Least-Squares Outlier Detection (LSOD) is an inlier-based outlier detection algorithm. The problem of inlier-based outlier detection is to find outliers in a set of samples (called the evaluation set) using another set of samples which consists only of inliers (called the model set). LSOD orders the samples in the evaluation set according to their degree of outlyingness. The degree of outlyingness is measured by the ratio of probability densities of evaluation and model samples. The ratio is estimated by the density-ratio estimation method uLSIF.
-
MATLAB implementation of LSOD:
LSOD.zip
- "LSOD.m" is the main function.
- "demo_LSOD.m" is a demo script.
-
Examples:
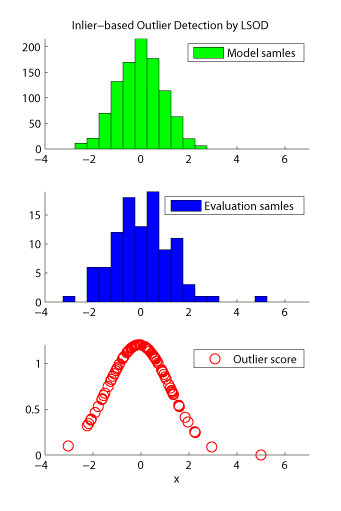
-
References:
-
Hido, S., Tsuboi, Y., Kashima, H., Sugiyama, M., & Kanamori, T.
Statistical outlier detection using direct density ratio estimation.
Knowledge and Information Systems, vol.26, no.2, pp.309-336, 2011.
[ paper ] -
Kanamori, T., Hido, S., & Sugiyama, M.
A least-squares approach to direct importance estimation.
Journal of Machine Learning Research, vol.10 (Jul.), pp.1391-1445, 2009.
[ paper ]
-
Hido, S., Tsuboi, Y., Kashima, H., Sugiyama, M., & Kanamori, T.
Maximum Likelihood Feature Selection (MLFS)
-
Maximum Likelihood Feature Selection (MLFS)
is a feature selection method for supervised regression and classification.
MLFS orders input features according to their dependence on output values.
Dependency between inputs and outputs is evaluated
based on an estimator of mutual information
called MLMI.
-
MATLAB implementation of MLFS:
MLFS.zip
- "MLFSP.m" is the main function.
- "demo_MLFS.m" is a demo script.
-
Examples:
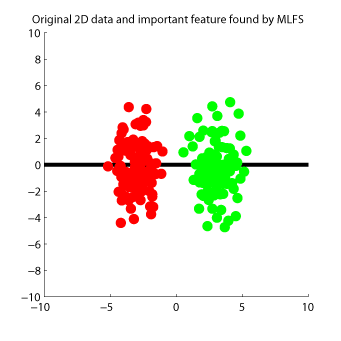
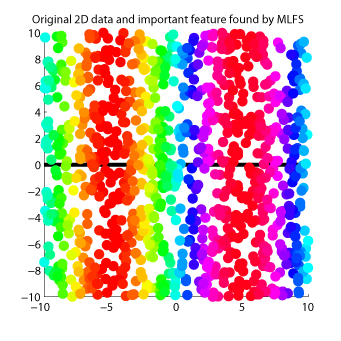
-
References:
-
Suzuki, T., Sugiyama, M., Sese, J. & Kanamori, T.
Approximating mutual information by maximum likelihood density ratio estimation,
In Y. Saeys, H. Liu, I. Inza, L. Wehenkel and Y. Van de Peer (Eds.), Proceedings of the Workshop on New Challenges for Feature Selection in Data Mining and Knowledge Discovery 2008 (FSDM2008) , JMLR Workshop and Conference Proceedings, vol. 4, pp.5-20, 2008.
[ paper ] -
Sugiyama, M., Suzuki, T., Nakajima, S., Kashima, H., von Bünau, P. & Kawanabe, M.
Direct importance estimation for covariate shift adaptation.
Annals of the Institute of Statistical Mathematics, vol.60, no.4, pp.699-746, 2008.
[ paper ]
-
Suzuki, T., Sugiyama, M., Sese, J. & Kanamori, T.
Least-Squares Feature Selection (LSFS)
- Least-Squares Feature Selection (LSFS) is a feature selection method for supervised regression and classification. LSFS orders input features according to their dependence on output values. Dependency between inputs and outputs is evaluated based on an estimator of squared-loss mutual information called LSMI.
-
MATLAB implementation of LSFS:
LSFS.zip
- "LSFSP.m" is the main function.
- "demo_LSFS.m" is a demo script.
-
Examples:
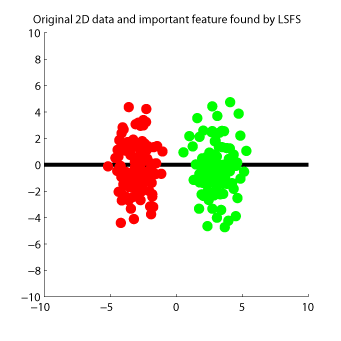
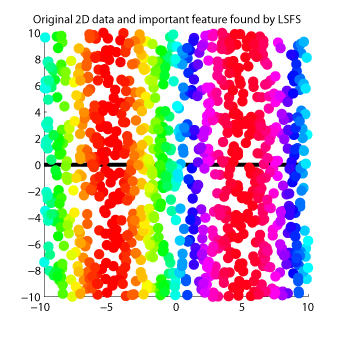
-
References:
-
Suzuki, T., Sugiyama, M., Kanamori, T., & Sese, J.
Mutual information estimation reveals global associations between stimuli and biological processes.
BMC Bioinformatics, vol.10, no.1, pp.S52, 2009.
[ paper ] -
Kanamori, T., Hido, S., & Sugiyama, M.
A least-squares approach to direct importance estimation.
Journal of Machine Learning Research, vol.10 (Jul.), pp.1391-1445, 2009.
[ paper ]
-
Suzuki, T., Sugiyama, M., Kanamori, T., & Sese, J.
Least-Squares Dimensionality Reduction (LSDR)
- Least-Squares Dimensionality Reduction (LSDR) is a supervised dimensionality reduction method. LSDR adopts a squared-loss variant of mutual information as an independence measure and estimates it using the density-ratio estimation method uLSIF. Thanks to this formulation, all tuning parameters such as the Gaussian width and the regularization parameter can be automatically chosen based on a cross-validation method. Then LSDR maximizes this independence measure (making the complementary features conditional independent of outputs) by a natural gradient algorithm.
-
MATLAB implementation of LSDR:
LSDR.zip
- "demo_LSDR.m" is a demo script.
-
Examples:
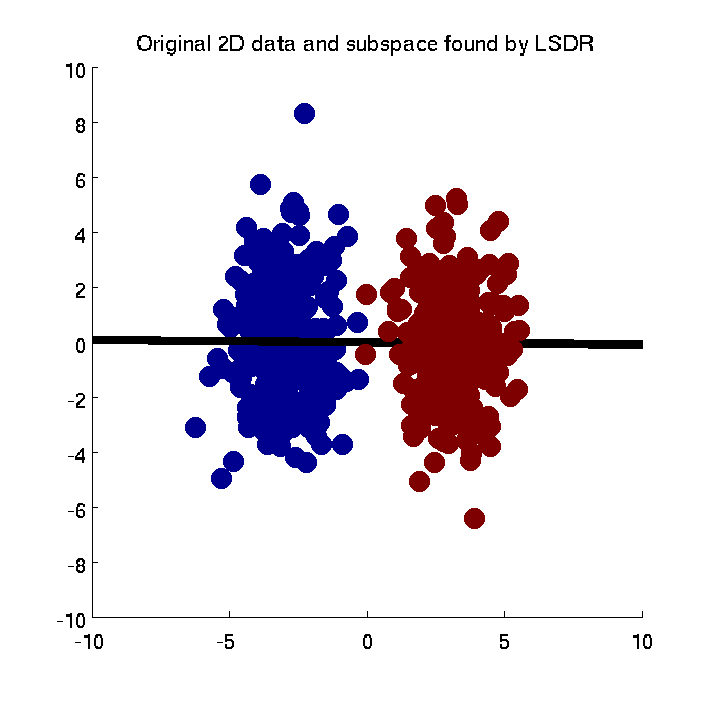
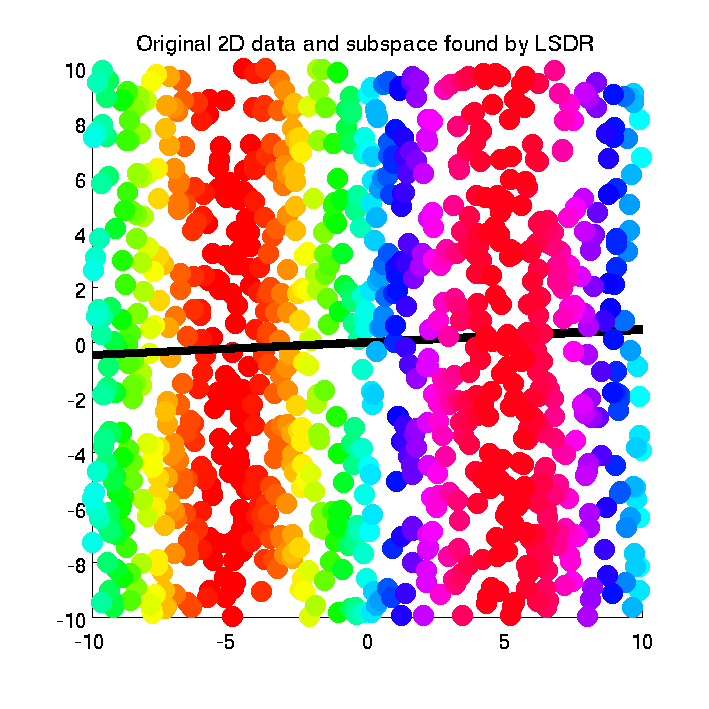
-
Reference:
-
Suzuki, T. & Sugiyama, M.
Sufficient dimension reduction via squared-loss mutual information estimation.
Neural Computation, vol.25, no.3, pp.725-758, 2013.
[ paper ]
-
Suzuki, T. & Sugiyama, M.
Least-Squares Quadratic Mutual Information Derivative (LSQMID)
- The Least-Squares Quadratic Mutual Information Derivative (LSQMID) is a supervised dimensionality reduction method. LSQMID aims to find a linear projection of input such that quadratic mutual information (QMI) between projected input and output is maximized. LSQMID directly estimates the derivative of QMI without estimating QMI itself. Then, an QMI maximizer is obtained by fixed-point iteration. An important property of LSQMID is its robustness against outliers. Moreover, all tuning parameters such as the Gaussian width and the regularization parameter can be automatically chosen based on cross-validation.
-
MATLAB implementation of LSQMID:
LSQMID.zip
- "demo_LSQMID_SDR.m" is a demo script.
-
Examples:
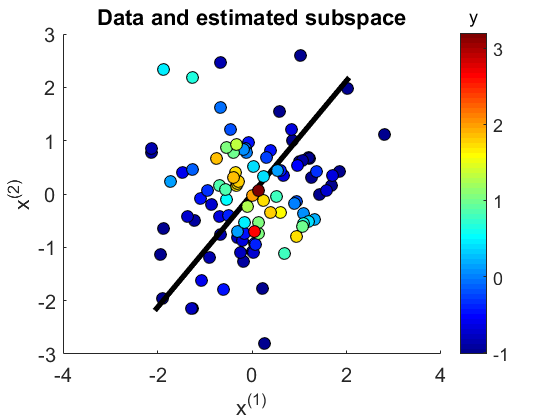
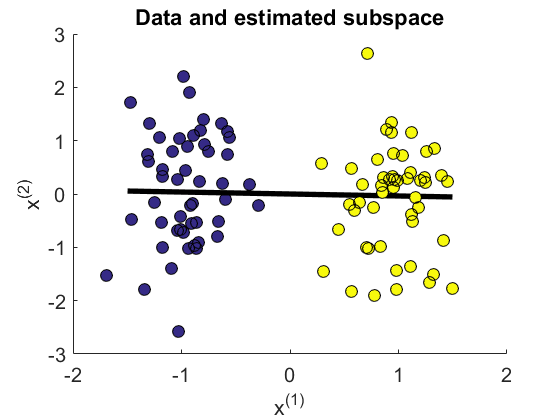
-
Reference:
-
Tangkaratt, V., Sasaki, H., & Sugiyama, M.
Direct estimation of the derivative of quadratic mutual information with application in supervised dimension reduction.
arXiv, 1508.01019, 2015.
-
Tangkaratt, V., Sasaki, H., & Sugiyama, M.
Local Fisher Discriminant Analysis (LFDA)
- Local Fisher Discriminant Analysis (LFDA) is a linear supervised dimensionality reduction method and is particularly useful when some class consists of separate clusters. LFDA has an analytic form of the embedding matrix and the solution can be easily computed just by solving a generalized eigenvalue problem. Therefore, LFDA is scalable to large datasets and computationally reliable. A kernelized variant of LFDA called Kernel LFDA (KLFDA) is also available.
-
MATLAB implementation of LFDA:
LFDA.zip
- "LFDA.m" is the main function.
- "demo_LFDA.m" is a demo script.
-
Examples:
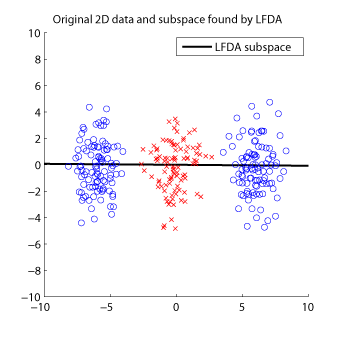
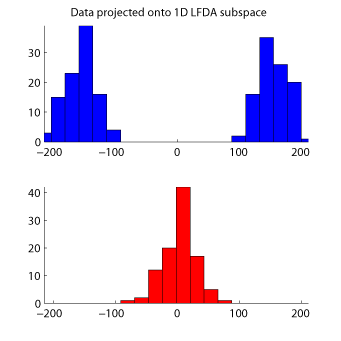
-
MATLAB implementation of KLFDA:
KLFDA.zip
- "KLFDA.m" is the main function.
- "demo_KLFDA.m" is a demo script.
-
Examples:
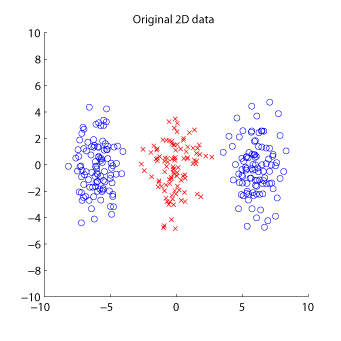
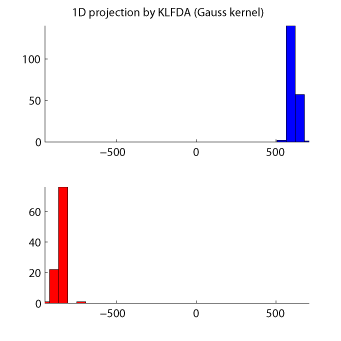
-
References:
-
Sugiyama, M.
Dimensionality reduction of multimodal labeled data by local Fisher discriminant analysis.
Journal of Machine Learning Research, vol.8 (May), pp.1027-1061, 2007.
[ paper ] -
Sugiyama, M.
Local Fisher discriminant analysis for supervised dimensionality reduction.
In W. W. Cohen and A. Moore (Eds.), Proceedings of 23rd International Conference on Machine Learning (ICML2006), pp.905-912, Pittsburgh, Pennsylvania, USA, Jun. 25-29, 2006.
[ paper, slides ]
-
Sugiyama, M.
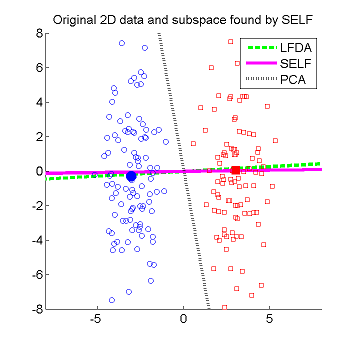
Semi-supervised Local Fisher discriminant analysis (SELF)
- Semi-supervised Local Fisher discriminant analysis (SELF) is a linear semi-supervised dimensionality reduction method. SELF smoothly bridges supervised Local Fisher Discriminant Analysis (LFDA) and unsupervised Principal Component Analysis (PCA), by which a natural regularization effect can be obtained when only a small number of labeled samples are available. SELF has an analytic form of the embedding matrix and the solution can be easily computed just by solving a generalized eigenvalue problem. Therefore, SELF is scalable to large datasets and computationally reliable. Applying the standard kernel trick allows us to obtain a non-linear extension of SELF called Kernel SELF (KSELF).
- When SELF is operated in the complete supervised mode, it is reduced to LFDA. However, its solution is generally slightly different from the one obtained by LFDA since nearest neighbor search (used for computing local data scaling in the affinity matrix) is carried out in a different manner: LFDA searches for nearest neighbors within each class, while nearest neighbor search in SELF is performed over all samples (including unlabeled samples). This is becuase SELF presumes that only a small number of labeled samples are available and searching for nearest neighbors within each class is not effective for capturing local data scaling in small sample cases. When SELF is operated in the complete unsupervised mode, it is reduced to PCA.
-
MATLAB implementation of SELF:
SELF.zip
- "SELF.m" is the main function.
- "demo_SELF.m" is a demo script.
-
Examples:
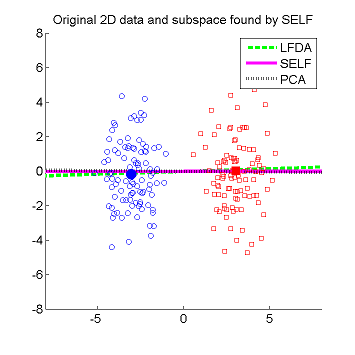
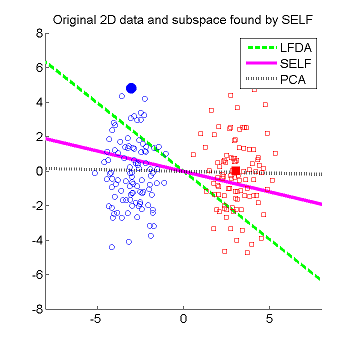
-
Reference:
-
Sugiyama, M., Idé, T., Nakajima, S., & Sese, J.
Semi-supervised local Fisher discriminant analysis for dimensionality reduction.
Machine Learning, vol.78, no.1-2, pp.35-61, 2010.
[ paper ]
-
Sugiyama, M., Idé, T., Nakajima, S., & Sese, J.
PU Classification
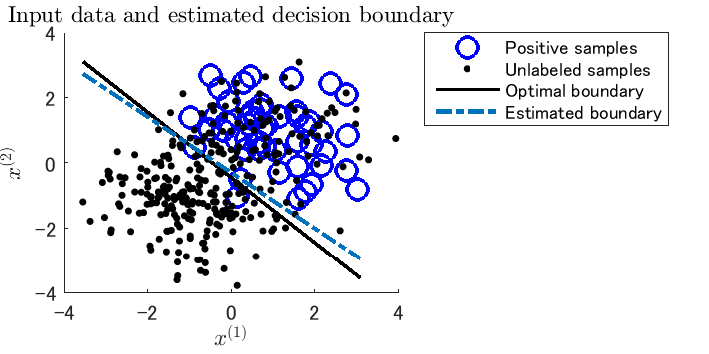
- Classification from positive and unlabeled samples, called PU classification, is aimed at learning the decision boundary between positive and negative samples only from positive and unlabeled samples.
-
MATLAB implementation of PU classification with the squared loss:
PU.zip
- "PU_SL.m" is a function for training a classifier.
- "demo.m" is a demo function.
-
Example:
-
References:
-
du Plessis, M. C., Niu, G., & Sugiyama, M.
Convex formulation for learning from positive and unlabeled data.
In F. Bach and D. Blei (Eds.), Proceedings of 32nd International Conference on Machine Learning (ICML2015), JMLR Workshop and Conference Proceedings, vol.37, pp.1386-1394, Lille, France, Jul. 6-11, 2015.
[ paper ] -
du Plessis, M. C., Niu, G., & Sugiyama, M.
Analysis of learning from positive and unlabeled data.
In Z. Ghahramani, M. Welling, C. Cortes, N. D. Lawrence, and K. Q. Weinberger (Eds.), Advances in Neural Information Processing Systems 27, pp.703-711, 2014.
(Presented at Neural Information Processing Systems (NIPS2014), Montreal, Quebec, Canada, Dec. 8-11, 2014)
[ paper ]
-
du Plessis, M. C., Niu, G., & Sugiyama, M.
PNU Classification
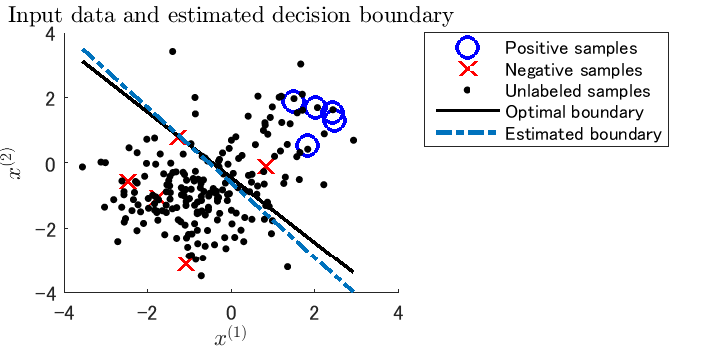
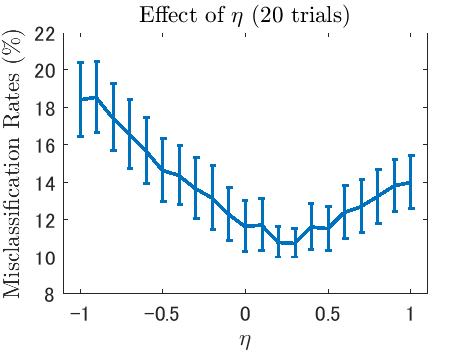
- PNU classification is a semi-supervised classification method that combines PN classification (classification from positive and negative samples, ordinary supervised classification) with PU classification (classification from positive and unlabeled samples) or NU classification (classification from negative and unlabeled samples). Unlike existing semi-supervised classification methods, PNU classification does not require any distributional assumptions such as the cluster assumption and the manifold assumption.
-
MATLAB implementation of PNU classification with the squared loss:
PNU.zip
- "PNU_SL.m" is a function for training a classifier.
- "demo.m" is a demo function.
-
Examples:
-
Reference:
-
Sakai, T., du Plessis, M. C., Niu, G., & Sugiyama, M.
Semi-supervised classification based on classification from positive and unlabeled data.
arXiv:1605.06955 [cs.LG]
[ paper ]
-
Sakai, T., du Plessis, M. C., Niu, G., & Sugiyama, M.
Least-Squares Conditional Density Estimation (LSCDE)
- Least-Squares Conditional Density Estimation (LSCDE) is an algorithm to estimate the conditional density function for multi-dimensional continuous variables. The solution of LSCDE can be computed analytically and all the tuning parameters such as the kernel width and regularization parameters can be automatically chosen by cross-validation.
-
MATLAB implementation of LSCDE:
LSCDE.zip
- "LSCDE.m" is the main function.
- "demo_LSCDE.m" is a demo script.
-
Examples:
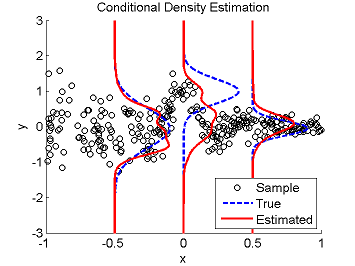
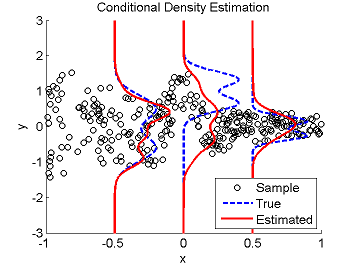
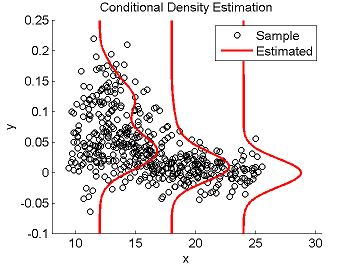
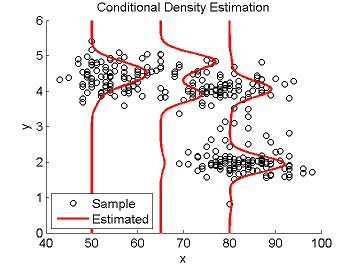
- References:
Least-Squares Probabilistic Classifier (LSPC)
- Least-Squares Probabilistic Classifier (LSPC) is a multi-class probabilistic classification algorithm. Its solution can be computed analytically in a class-wise manner, so it is computationally very efficient.
-
MATLAB implementation of LSPC:
LSPC.zip
- "demo_LSPC.m" is a demo script.
-
Examples:
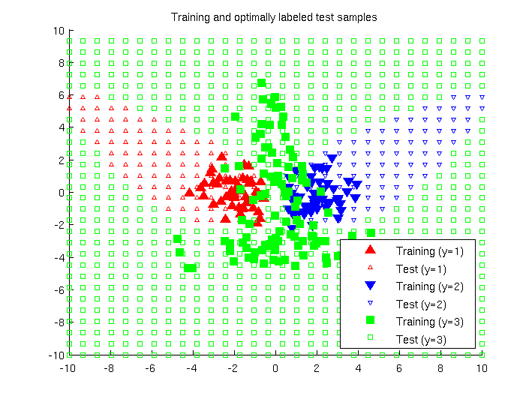
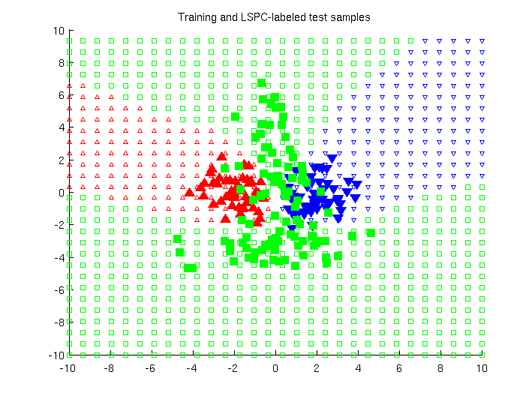
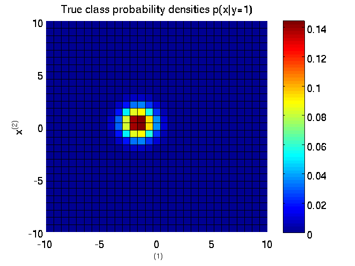
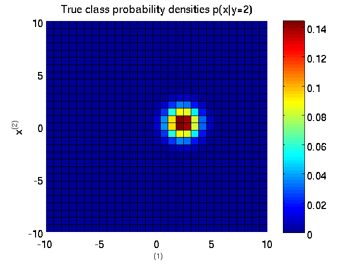
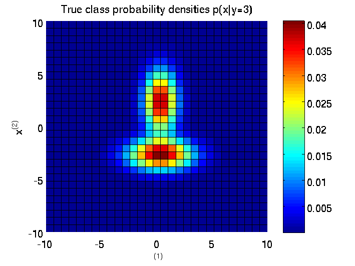
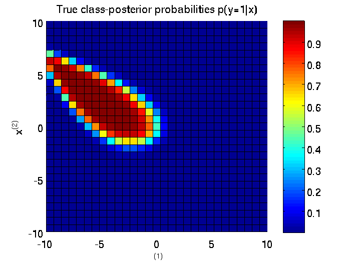
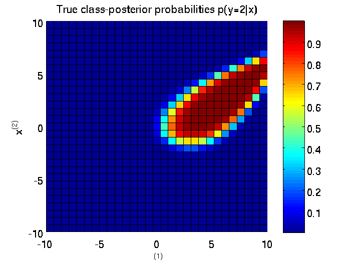
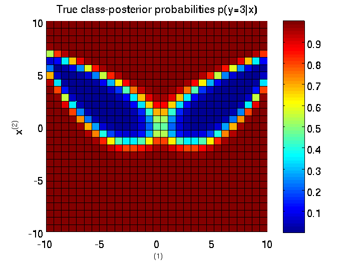
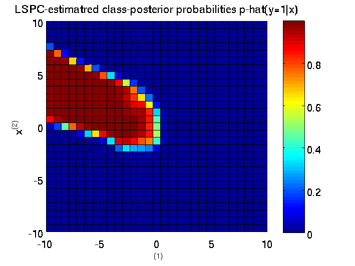
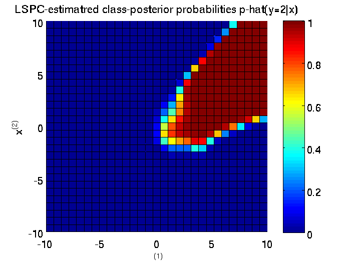
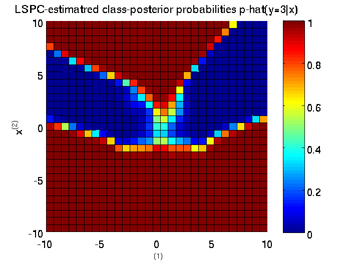
-
References:
-
Sugiyama, M.
Superfast-trainable multi-class probabilistic classifier by least-squares posterior fitting.
IEICE Transactions on Information and Systems, vol.E93-D, no.10, pp.2690-2701, 2010.
[ paper (revised version) ]
-
Yamada, M., Sugiyama, M., Wichern, G., & Simm, J.
Improving the accuracy of least-squares probabilistic classifiers.
IEICE Transactions on Information and Systems, vol.E94-D, no.6, pp.1337-1340, 2011.
[ paper ]
-
Sugiyama, M.
Least-Squares Independence Test (LSIT)
- Least-Squares Independence Test (LSIT) is a method of testing the null hypothesis that paired (input-output) samples are independent. LSIT adopts a squared-loss variant of mutual information as an independence measure and estimates it using the density-ratio estimation method uLSIF. Thanks to this formulation, all tuning parameters such as the Gaussian width and the regularization parameter can be automatically chosen based on a cross-validation method.
-
MATLAB implementation of LSIT:
LSIT.zip
- "demo_LSIT.m" is a demo script.
-
Examples:
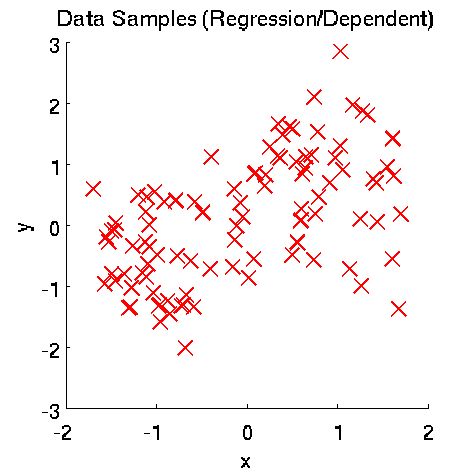
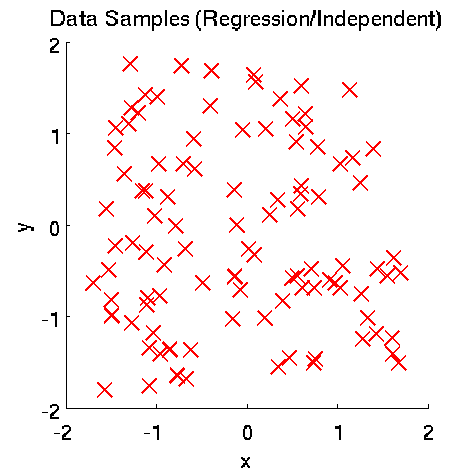
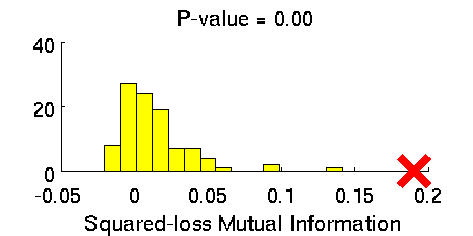
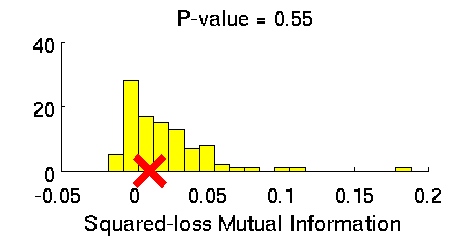
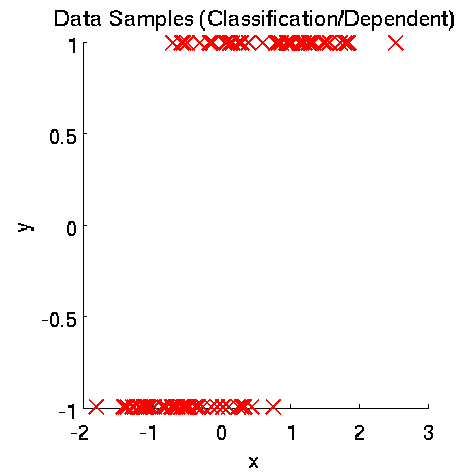
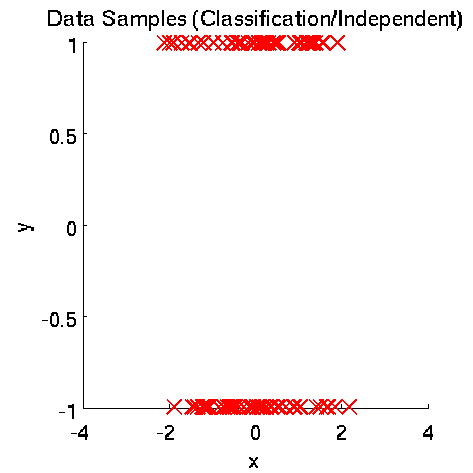
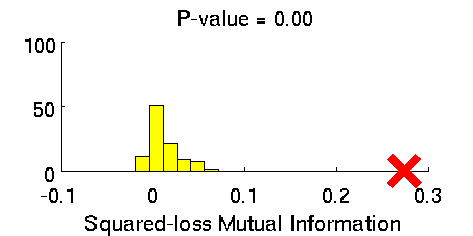
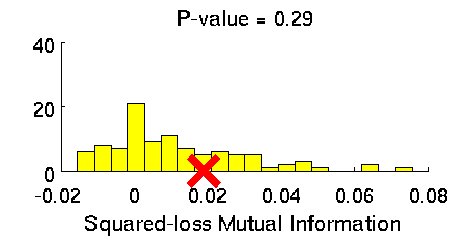
- References:
Least-Squares Two-Sample Test (LSTT)
- Least-Squares Two-Sample Test (LSTT) is a method of testing the null hypothesis that two sets of samples are drawn from the same probability distribution. LSTT adopts a squared-loss variant of mutual information as an independence measure and estimates it using the density-ratio estimation method uLSIF. Thanks to this formulation, all tuning parameters such as the Gaussian width and the regularization parameter can be automatically chosen based on a cross-validation method.
-
MATLAB implementation of LSTT:
LSTT.zip
- "demo_LSTT.m" is a demo script.
-
Examples:
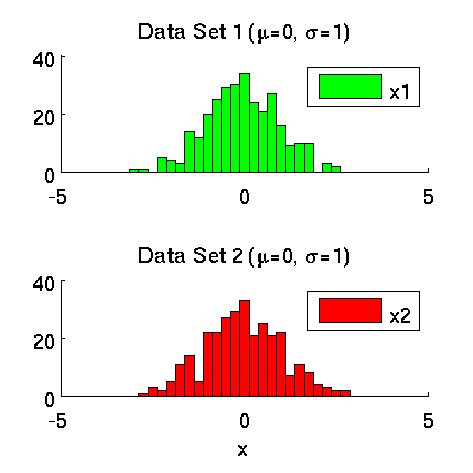
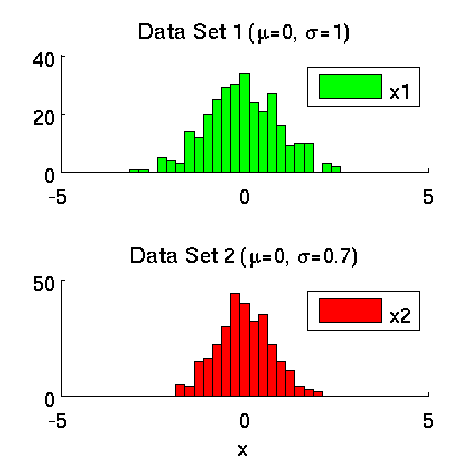
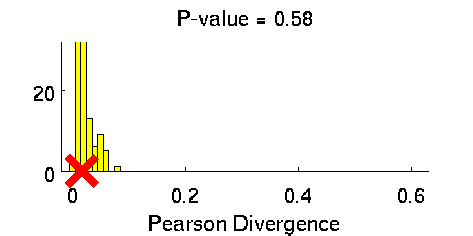
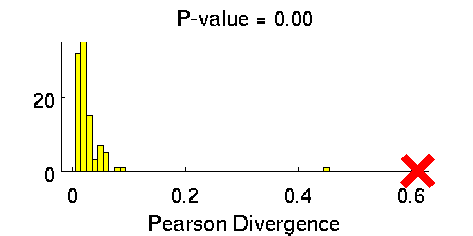
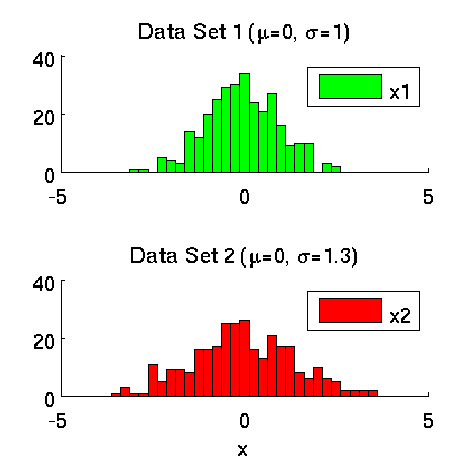
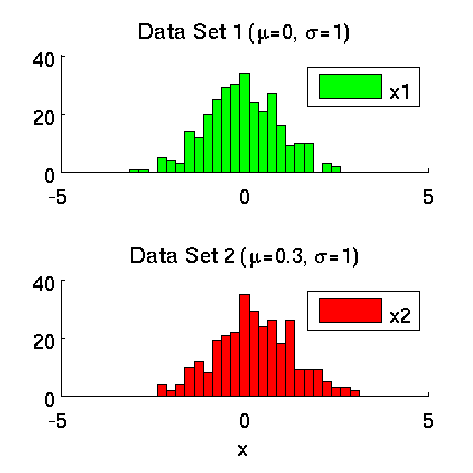
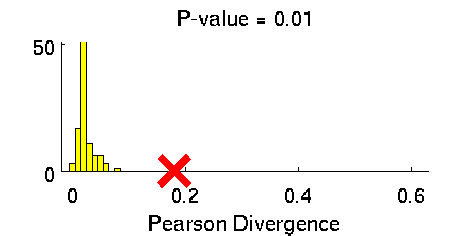
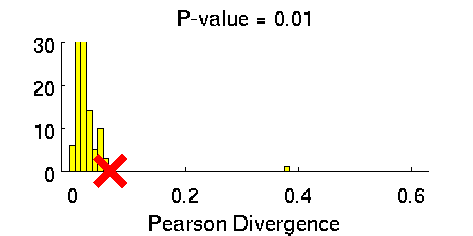
-
References:
-
Sugiyama, M., Suzuki, T., Itoh, Y., Kanamori, T., & Kimura, M.
Least-squares two-sample test.
Neural Networks, vol.24, no.7, pp.735-751, 2011.
[ paper ]
-
Sugiyama, M., Suzuki, T., Itoh, Y., Kanamori, T., & Kimura, M.
SMI-based Clustering (SMIC)
-
SMI-based Clustering (SMIC)
is an information-maximization clustering algorithm
based on the squared-loss mutual information (SMI).
SMIC is equipped with automatic tuning parameter selection based on an SMI estimator called
least-squares mutual information (LSMI).
-
MATLAB implementation of SMIC:
SMIC.zip
- "SMIC.m" is the main function.
- "demo_SMIC.m" is a demo script.
-
Examples:
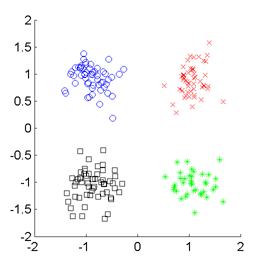
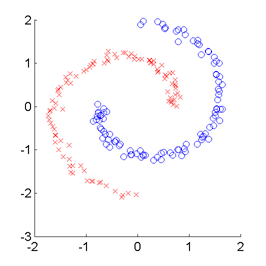
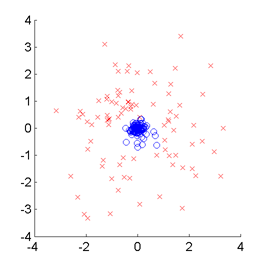
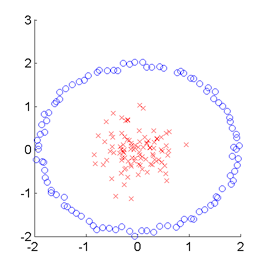
-
References:
-
Sugiyama, M., Gang, N., Yamada, M., Kimura, M., & Hachiya, H.
Information-maximization clustering based on squared-loss mutual information.
Neural Computation, to appear.
[ paper ] -
Sugiyama, M., Yamada, M., Kimura, M., & Hachiya, H.
On information-maximization clustering: tuning parameter selection and analytic solution.
In L. Getoor and T. Scheffer (Eds.), Proceedings of 28th International Conference on Machine Learning (ICML2011), pp.65-72, Bellevue, Washington, USA, Jun. 28-Jul. 2, 2011.
[ paper, slides ]
-
Sugiyama, M., Gang, N., Yamada, M., Kimura, M., & Hachiya, H.
Variational Bayesian Matrix Factorization (VBMF)
- Givan a fully-observed noisy matrix V, Variational Bayesian Matrix Factorization (VBMF) denoises the matrix V under a low-rank assumption. Based on the empirical Bayesian method, VBMF automatically determines all the tuning parameters such as the rank of the denoised matrix, the noise variance, and the prior variances.
-
MATLAB implementation of VBMF:
VBMF.zip
- "VBMF.m" is the main function.
- "demo_VBMF.m" is a demo script.
-
Examples:
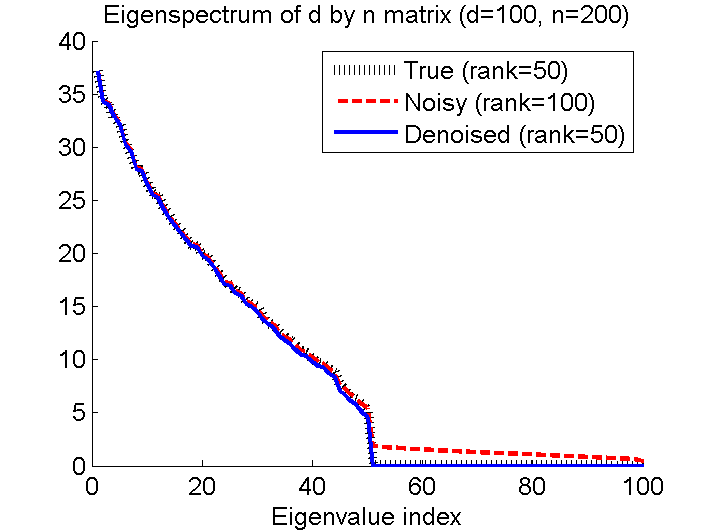
-
References:
-
Nakajima, S., Sugiyama, M., & Babacan, D.
Global solution of fully-observed variational Bayesian matrix factorization is column-wise independent.
In J. Shawe-Taylor, R. S. Zemel, P. Bartlett, F. C. N. Pereira, and K. Q. Weinberger (Eds.), Advances in Neural Information Processing Systems 24, pp.208-216, 2011.
(Presented at Neural Information Processing Systems (NIPS2011), Granada, Spain, Dec. 13-15, 2011)
[ paper ] -
Nakajima, S., Sugiyama, M., & Tomioka, M.
Global analytic solution for variational Bayesian matrix factorization.
In J. Lafferty, C. K. I. Williams, R. Zemel, J. Shawe-Taylor, and A. Culotta (Eds.), Advances in Neural Information Processing Systems 23, pp.1759-1767, 2010.
(Presented at Neural Information Processing Systems (NIPS2010), Vancouver, British Columbia, Canada, Dec. 6-11, 2010)
[ paper, poster ]
-
Nakajima, S., Sugiyama, M., & Babacan, D.
Masashi Sugiyama (sugi [at] k.u-tokyo.ac.jp)